The 21 of Growth

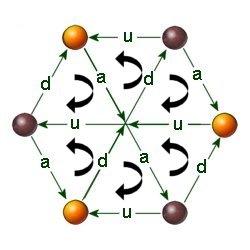
Where there is growth of being, the sixty-four choices are limited, for the choices which mirror themselves return to the previous state, building the pattern of life-one, two, three, five, eight, thirteen, twenty-one—restricting the sixty-four of multiplication to the twenty-one of growth.
Book of Jubilee, Chapter 6.

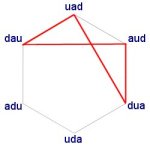
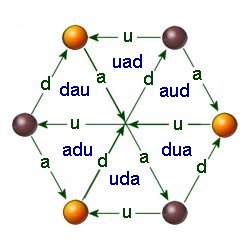
When constructors are arranged so that the last force in one is the same as the first force in the next, there is always a choice of two. For example, DAU or DUA could come after UAD. If we add a third constructor, then UAD or UDA could come after DAU, and AUD or ADU could come after DUA, giving a total of four possibilities:

UAD DAU UAD or
UAD DAU UDA or
UAD DUA AUD or
UAD DUA ADU

As we add more constructors, the choices double each time: 1, 2, 4, 8, 16, 32, 64 by the time we get to seven constructors in a row. This is a rule of division or multiplication.

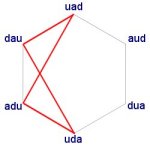
But consider the possibilities for three constructors we looked at above. In the first possibility listed, UAD DAU UAD, the constructor UAD is repeated. This is because UAD is mirrored to make DAU and then this is mirrored back to repeat UAD. If we prune the possibilities when this happens, we get a different set of possibilities. Instead of 1, 2, 4, 8, 16, 31, 64 we get 1, 2, 3, 5, 8, 13, 21. This is a rule of growth.

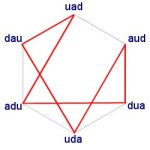
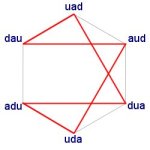
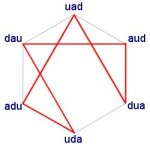
The tree diagram below shows this process. The red coloured constructors are the ones pruned from this ‘multiplication’ tree because they mirror and mirror back as described above.

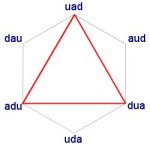
There are still some repetitions of constructors in the 21 possibilities. For example, one of the possibilities is UAD DAU UDA ADU UAD DAU UDA, which has many repeats, although none that are caused by mirror-and-mirror-back. The ones that have no repetitions (except that they end where they start) are coloured green, and of course these are the three cosmoses of the fourth world (see the article on worlds and cosmoses).

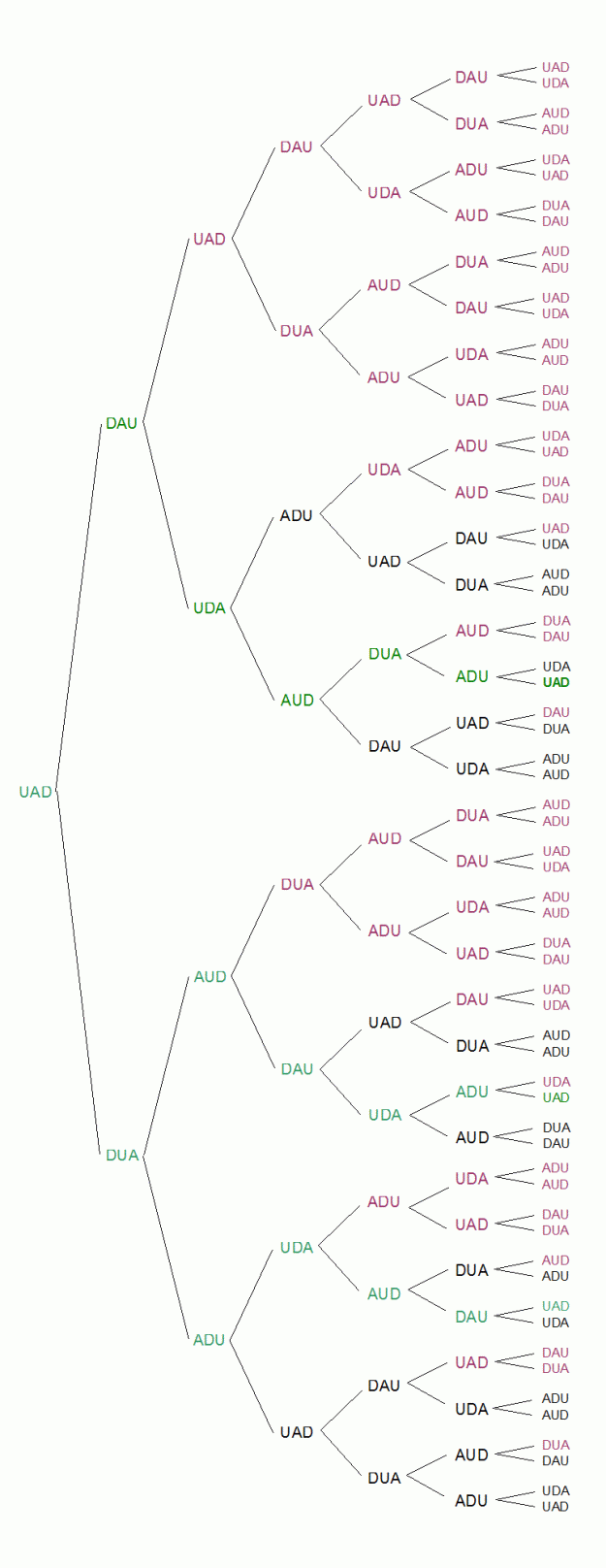
The tree of growth, 1, 2, 3, 5, 8, 13, 21, is of course the Fibonacci sequence, which is connected with organic growth.

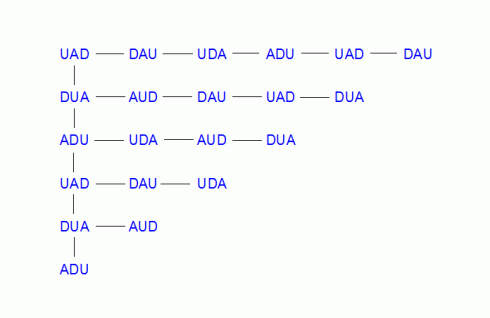
The number 21 comes about from this tree of growth, but also appears in other ways. For example, seven times three gives 21: we line up 7 combinations of constructors made from 3 forces. How many constructors appear in the tree altogether? Leaving out the original, each appears 21 times.

Another way that 21 comes about is the law of addition: 1+2+3+4+5+6 = 21. The sequence here is 1, 3, 6, 10, 15, 21, the triangular numbers. These make the pyramids described in the book of Jubilee:

O
O O
O O O
O O O O
O O O O O
O O O O O O

The book describes a way of making a square of 64 constructors. My interpretation of this for the square beginning with UAD is shown below.

I’ve shown the relationships of mirror (m) and follower (f) that are described. Any route through the square that is consistent with the arrows shown is bound to follow a path in the tree of growth, because each arrow represents a move to a mirror or to a follower, and there are no mirror-followed-by-mirror paths. To take a random example, moving from the top left of the square: from UAD go down to DUA, go down to ADU, go right to UDA, go up to AUD, go up to DAU. This takes us along one of the green paths in the tree.

We can superimpose pyramids on this square. Here is one example, showing the pyramid starting from UAD in the top left of the square.

The paths from the growth tree that are in this pyramid are illustrated below. Clearly, some of the possibilities in the 1, 2, 3, 5, 8, 13 layers of the growth tree are not included in the pyramid, which only contains 1, 2, 3, 4, 5, 6.

The square of 64 contains a pyramid for each constructor,  “In the first column three descending; in the third column three ascending“. These are shown below:

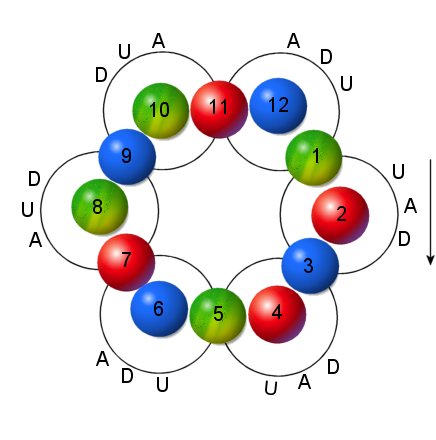
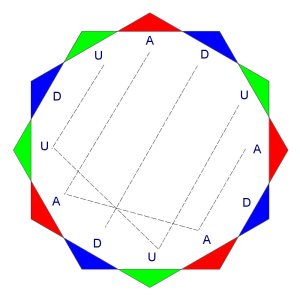
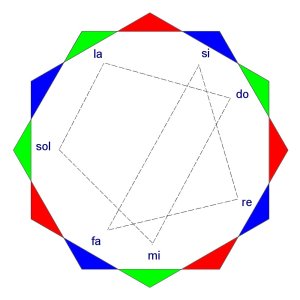
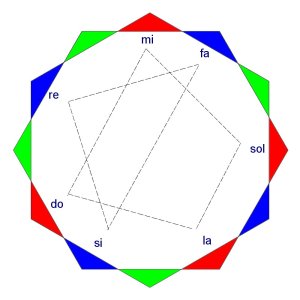
The square of 64 constructors has within it 24 self-completing sequences. Each of them is one of the 3 cosmoses in the fourth world, but starting on different constructors. As discussed before, each of these sequences can be seen as an octave.  The 24 are shown in the diagram below, labelled 1-24 by the starting point.  The self-completing sequence is illustrated for  1, 6, 7, 12, 12, 18, 19 and 24. The others are not drawn.

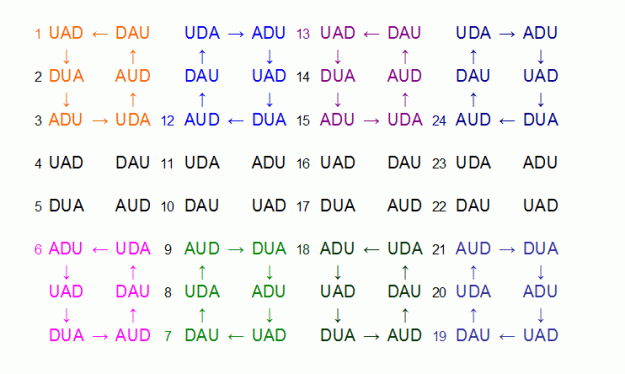
Within a single pyramid of 21, there are 4 complete octaves, but one is a duplicate of one of the others. For example, in the pyramid discussed above, depending from UAD in the top-left, the octaves labelled 1,2,3 and 12 are wholly within the pyramid. 12 is a duplicate of 3, starting in a different place. The remaining three octaves within the pyramid are the three cosmoses in the fourth world.

 

The Octave

“The octave is the means by which the three mothers set up the process of rhythmic response. It is the law that to each action there is an equal and opposite reaction.”
Book of Jubilee, Chapter 5

The octave arises from the internal structure of the fourth world cosmoses. The cosmoses are described in an earlier post, and are each formed as a cycle of constructors, the 3rd force in one constructor becoming the first force of the next. For example, the fifth cosmos dependant from UAD is:

UAD-DAU-UDA-AUD-DUA-ADU

In this pattern there are a total of 6 x 3=18 forces, but a more compact way of writing the pattern is to only write the repeating forces once, so that UAD-DAU would become UADAU, with the D in the middle serving as the last force in UAD and the first in DAU. Doing this to the entire cosmos gives the sequence:

U A D A U D A U D U A D

The process is more clearly shown in a circular figure, since it runs in cycles.  In the figure below, the same cosmos is illustrated, with the forces arranged around a circle, moving clockwise from the right hand side, starting with UAD, which is numbered 1, 2, 3, and ending with ADU, numbered 11,12,1.

Energy steps within the octave

There are patterns within the cycle of twelve mothers. For example, the unifying mother appears in position 1, 5, 8 and 10, separated from each other by steps of 3 then 2 and then 1. The pattern is reversed for the affirming mother, which takes increasing steps, whilst the denying mother is evenly spaced in the cycle. These patterns are illustrated below:

“The mother which starts each octave, the first in the initiating constructor, possesses the greatest energy, and this energy runs down in jumps of three, two, and one steps. The second mother in the initiating constructor starts slowly and builds up to higher energies by one, two and three steps. The mother in the third place maintains the same strength throughout the six constructors in steps of two, two and two.”

The Notes of the Octave

The pattern of the octave is the same as a musical octave, with seven notes progressing from the note do to the same note at a higher frequency:

do – re – mi – fa – sol – la – si – do

The spacing of the notes in an octave is not constant. The mi-fa interval and the si-do interval are half as wide as the others (semi-tones rather than full tones). This same pattern is seen in the octave embedded in the sequence of twelve mothers.

The full tone intervals appears with another mother between the two notes. For example, the first two notes of the octave (do-re) are formed by the first three mothers in the sequence:

U (the do note) – A (the interval) – D (the re note)

The semi-tone intervals appear with no third mother between the notes. For example, the first shortened interval (mi-fa) is formed by:

U (the mi note) – D (the fa note)

In many traditions the octave is seen as a model of cosmological processes, with the shortened intervals indicative of places where a change of pace or direction might occur.

These are explained in the Book of Jubilee as a consequence of the way the mothers are arranged:

“When the third mother follows the first mother, the effect is to slow down process; when it leads the first mother, process is speeded up. The places where the third mother stands next to the first mother are the sixth, the ninth and the twelfth. In the sixth position it slows process down; in the ninth it both speeds up and slows down, so there is no effect; but in the twelfth process speeds up to start the next octave.”

One way to think about this is as follows:

This particular octave is about the interaction of two mothers, U and D; all of the notes are centred on these two.

Where the interaction between the two is mediated by the third mother, a smooth interaction takes place, and we get the full tone steps UAD (at do-re and la-si) and DAU (at re-mi and fa-sol).

Where the two mother meet without the mediation of the third, we get a different type of interaction: the UD at mi-fa slows the process, and the DU at si-do speeds up the process. In the centre of the octave we get both occurring together: UDU at sol-la.

Mutually Maintaining Octave

Each fourth world cosmos contains two octaves. The one we have just looked at is complemented by a second octave starting halfway round the circle in position 7:

This octave has the same pattern, but is about the interaction of A and D, mediated this time by U. The two octaves within the cosmos interlock and maintain each other.

Some questions

Some questions to ponder: How many octave patterns are there all together, taking into account all of the fourth world cosmoses? How do the two octaves maintain each other? What would they sound like? If there was a movement for the octave, a dance perhaps, what would it be like?

Worlds and Cosmoses

“Seven cosmoses depend from each constructor.”
Book of Jubilee, Chapter 3

Here is one understanding of the way in which cosmoses and worlds arise from the six constructors. Each constructor is a particular combination of the three mothers. For example the constructor called contraction, UAD, has the unifying mother in the first place, the affirming mother in the second and the denying mother in the third place.

The constructors make cosmoses by joining together head to tail – that is, the final mother in one become the first mother in the next. A cycle of constructors each connected to the next in this way forms a cosmos.

The First Cosmos in the First World

The first cosmos depending from UAD is the constructor and its mirror DAU. The cosmos forms an endless cycle of UAD-DAU–UAD-DAU-UAD… Contract-Repeat-Contract-Repeat… reflecting back and forth.

There will be two other similar cosmoses made of other mirror pairs. These three cosmoses together form the first world:

“The first world’s beings are the substance of that world, the hierarchical world. They come into being out of the six by combination of any two mirrors. Such beings do not yet have perceptible existence. They are the seeds of the multiverse, one turning one way, one the other. From their pairings are formed the bases of growth, compression and change. As yet time and space do not arise; in themselves they contain all the possible creations. It is the world of Gods—Gods in the likeness of fiery serpents or infinite vortices or the Miracle Gods who change the aspect of all received by them. It is a world of mirrors, ‘in our own likeness’.”

The Second Cosmos in the Second World

The second cosmos is formed by three constructors UAD-DUA-ADU.

There is another cosmos formed from the other three constructors: UDA-AUD-DAU. These two cosmoses together form the second world:

“The second world’s beings are also identical with the substance of their world. It is the substance of time and space, the world of resilience. When time expands, space expands; when time changes, space changes. The smaller the object, the faster its time; the greater the object’s extent, the greater its cycle of time. Wheels creating, adapting and replicating, spinning in all directions, weaving the fabric of space; Orbs expanding, shrinking and mutating, forming the extent and substance of all creations; each is dependent on the other. In this world all the possible universes are laid down in possible extent and possible duration. Here is the world of birth and death, the multiverse.”

Cosmoses 3 & 4 in the Third World

The third and fourth cosmoses dependant from UAD are each formed by four constructors:
UAD-DUA-AUD-DAU and ADU-UAD-DAU-UDA.

                

These two, together with a third cosmos of four constructors excluding UAD form the third world:

The denizens of the third world, the world of growth, are of two types, one in which a God conceals a follower’s God, and one in which a God is concealed by a leader’s God. In each the other lies hidden: it is a world of appearances, a world of duality where the serpents of growth are hidden in change or compression, the heralds of change are hidden by compression or growth, the vortices of compression are hidden in growth or change. It is the world of universes dependent on one constructor.

Cosmos 5,6,7 in the Fourth World

There are three cosmoses made of all six constructors:
UAD-DAU-UDA-AUD-DUA-ADU
UAD-DUA-ADU-UDA-AUD-DAU
UAD-DUA-AUD-DAU-UDA-ADU

When drawn out, each of them has a similar shape, reminiscent of an enneagram – of which more later.

    

These three together make the fourth world:

“The fourth world, the world of structure, is inhabited by three types of material beings. In one the denying is fixed, in another the affirming has become active, and in the third the unifying has acquired material existence. They correspond to those material beings in whom only what they receive from outside exists, those beings in whom what is outside of themselves has to be related to what is inside them, and those beings who impose on the outside their internal worlds of possibilities. All three possess within them the other three worlds in due proportion, two parts from the first, two from the second and two from the third: in all these living beings the possibility exists to perceive the whole of creation.”

A good starting point for working with the worlds and cosmoses is to write down your own list of all the combinations from each constructor. How many are there, and why just that number? Which are repeated, and how many times? Why?

Consider the patterns within each cosmos. For example, the third world cosmoses have mirrors within them. What are their relationships? How much of the description of each world do you think comes from the patterns?

Formation of the Constructors

“Three asleep, the Gate, three awake – these seven are the seven potencies which, separated and now conscious of one another, bring into perceptible existence the servants, the constructors of creation.”
Book of Jubilee, Chapter 2

Here is one arrangement of the seven potencies or pillars of the Temple: the three awake standing opposite the three asleep, with the Gate in the centre.

The motion of the three forces, the affirming, denying and unifying, create six swirlings in the spaces between the pillars.

Each of the swirlings is made by the three forces in a different order. Each swirling starts with a force that flows around the edge of the Temple, from one pillar to the one next to it, from one awake to one asleep. The middle force flows into the centre, from the one asleep to the gate, and the final force flows out again, from the gate to the one awake.

On this way the pattern is formed of the six constructors.

The arrangements of the constructors are described in Chapter 3. The first one is formed from the unifying, denying and affirming mother in that order: UDA, and is called Creation. Next to it in the Temple is it’s mirror, where the order of forces is reversed: ADU, and this is called Expansion. The order of the constructors follows around the Temple:

UDA – Creation
DUA – Transformation
AUD – Reception
UAD – Contraction
DAU – Repetition
ADU – Expansion